In het vorige artikel heb ik aandacht besteed aan een recente publicatie van de hand van een team onderzoekers van en rond TU Delft. Ik eindigde toen met de teleurstellende constatering dat het blijkbaar niet mogelijk leek om me op korte termijn aan de onderliggende data van de paper te helpen.
Intussen heb ik enkele malen contact gehad met de auteur die de communicatie verzorgt, en ik kreeg na wat ontwijkende antwoorden te horen: “Just a matter of lack of time. There was indeed a misunderstanding within the authors team. Of course those data were supposed to be online since the beginning! Now it’s holiday season, so things have to wait. We won’t forget to make them available.” Kortom: ik moet de academische vakantietijd afwachten totdat er tijd is om de gevraagde data te verschaffen. Intussen heb ik me (samen met Jan Ruis) op de cijfers gestort die wél beschikbaar zijn: de gemeten zeespiegelhoogten.
Fig.1 Reactie Hans Erren (LinkedIn)
Ook andere mensen houden zich intussen met dat Delft-rapport bezig. Geofysicus Hans Erren wees (figuur 1) op het grote verschil in lengte van de tijdreeksen vóór en na de ‘breuk’ in 1993: “What I would like to see as robustness test for the trend of the last 27 year is a plot of all 27 year window trends over the entire century time span.” Omdat in de paper de periode ná de vermeende breuk in 1993 loopt van 1994 t/m 2018 ga uit van een periode van 25 jaren. Figuur 2 toont de jaarlijkse gemeten zeespiegelhoogte (PSMSL) van het ensemble van de 6 hoofdstations Delfzijl, Harlingen, Den Helder, IJmuiden, Hoek van Holland en Vlissingen in de periode 1919-2018.
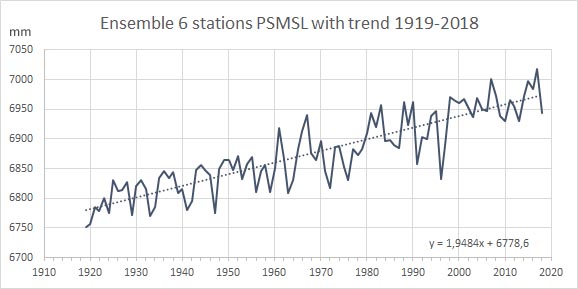
Fig.2 Data: PSMSL
De streepjeslijn is de lineaire trend en heeft een helling van 1,95 mm/jaar. Van de PSMSL data is vervolgens onderstaande grafiek gemaakt met de trend over windows van telkens 25 jaren, van 1919 t/m 2018.
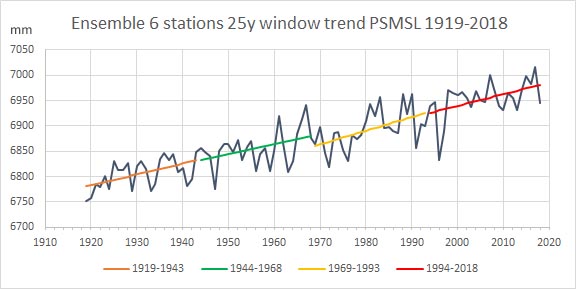
Fig.3 Data: PSMSL
Voor elk van de vier 25-jarige windows waarin de totale door Delft gebruikte periode kan worden ingedeeld is de lineaire trend bepaald en weergegeven met de gekleurde lijnstukken. Te zien is dat er op het oog nauwelijks verschillen in trend zijn tussen drie van de vier windows, alleen de trend van de periode 1969-1993 is verhoogd.
Erren schreef: “ Also there is good sea level data available before 1920. Please consider the conclusions of Kyra van Onselen about short period trends.” Hier is die verlengde periode, van 1894 t/m 2018, met wederom de trend over windows van 25 jaren:
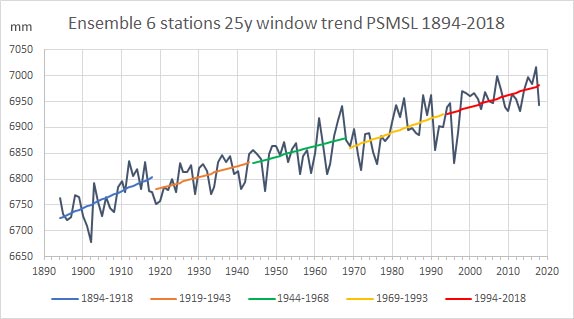
Fig.4 Data: PSMSL
Het eerste window van 1894 t/m 1918 vertoont duidelijk een verhoogde trend ten opzichte van de andere windows.
Bovenstaande trendgrafieken van de figuren 3 en 4 zijn gebaseerd op de officiële gemeten getijdedata van PSMSL. Niet te verwarren met het door de Delftse auteurs ‘gecorrigeerde’ sea level signal in figuur 3 van de publicatie waarop ze hun versnellingsdetectie hebben toegepast.
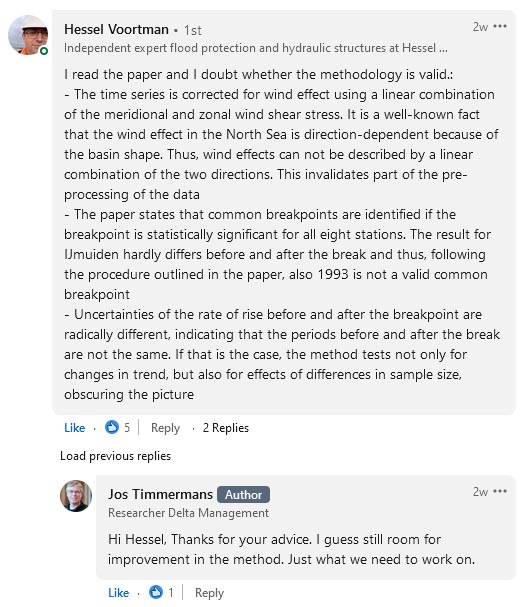
Fig.5 Reactie Hessel Voortman (LinkedIn)
Hessel Voortman, onafhankelijke consultant op het gebied van kustverdediging, reageerde ook op het Delftse rapport (figuur 5). Zijn commentaar is duidelijk: de gehanteerde methodiek deugt op een aantal punten niet. Volgens Voortman is het gebruik van zonale en meridionale windstress-data zoals gebruikt door de auteurs voor het corrigeren van de getijdemeetreeksen onjuist, omdat de vorm van het Noordzeebekken het windeffect richtingsgevoelig maakt. Daarmee zou de bodem onder het onderzoek uit vallen. Het proefschrift van Voortman levert interessant leesvoer.
In de Delftse studie wordt gesteld dat gemeenschappelijke breekpunten worden geïdentificeerd als het breekpunt statistisch significant is voor alle acht stations. Voortman stelt terecht vast dat de resultaten voor IJmuiden vóór en na de breuk nauwelijks van elkaar verschillen, en dat er dus in 1993 geen sprake is van een gemeenschappelijk breekpunt. Net als Hans Erren levert ook Voortman kritiek op de lengte van de gemeten periodes voor en na 1993. De Delftse methode toetst volgens hem daardoor niet alleen op trendveranderingen maar ook op verschillen in steekproefgrootte.
Jippe Hoogeveen bekeek de door de Delftse groep gebruikte methodiek en verbaasde zich onder andere over het feit dat men de nodale cyclus met een factor 1 aftrekt in plaats van er regressie op toepast. De nodale cyclus is een maancyclus met een periodiciteit van 18,61 jaar die een aanzienlijke invloed heeft op de zeespiegel. Voor wat betreft de factor wind zou het beter zijn die eerst voor elke dag te kwadrateren en daarna het gemiddelde te nemen, in plaats van de maandgemiddelden te kwadrateren.
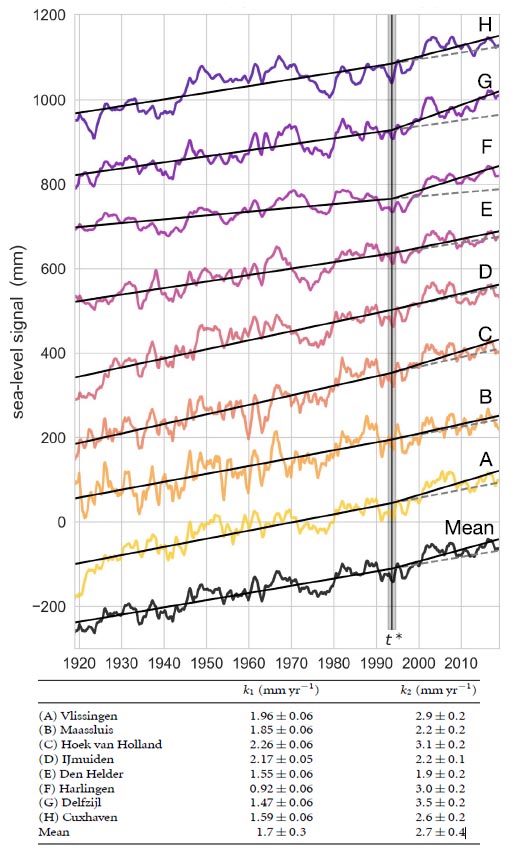
Fig. 6 Bron: Bron: Steffelbauer et al 2022
Aanzienlijke problemen ziet Hoogeveen opduiken in de manier waarop de auteurs dat gemeenschappelijk breekpunt vaststellen in het begin van de jaren negentig. De Delftse onderzoekers berekenen de trend vóór en na 1993 inclusief betrouwbaarheidsintervallen en concluderen dan dat die trends significant verschillen. Hoogeveen stelt echter dat die berekende betrouwbaarheidsintervallen niet correct zijn. De onderzoekers hebben in een eerdere stap de regressie gedaan om de invloed van de wind uit het signaal te halen. Wat ze nu laten zien in de publicatie (figuur 6) is het residu, maar dan zonder veel ruis. Vervolgens berekenen de auteurs op basis van dit residu de betrouwbaarheidsintervallen, maar volgens Hoogeveen mag dit niet zo maar. Immers, het betrouwbaarheidsinterval wordt veel kleiner als je alle ruis eruit haalt, maar er verandert niets aan de data zelf. Omdat de betrouwbaarheidsintervallen op deze manier veel kleiner worden gemaakt, verschillen die trends significant.
Om toch te kunnen rekenen aan gecorrigeerde data heeft Hoogeveen de Delftse regressiemethodiek toegepast op het ensemble van de 6 Nederlandse hoofdstations. Hij vindt vóór 1993 als trend 1,75 ± 0,3 mm jaar en na 1993 als trend 2,57 ± 1,45 mm/jaar. Dit verschilt niet significant. Het grote verschil is dat de trend ná 1993 een veel groter betrouwbaarheidsinterval heeft dan in het onderzoek van Delft. Dat is logisch, want als men de trend niet van 1993-2018 maar van 1993-2017 berekent, dan stijgt hij al tot maar liefst 2,84 ± 1,54 mm/jaar. Dat geeft goed aan hoe groot de onzekerheid is.
Ook is het opvallend dat in de tabel van figuur 6 hierboven de onzekerheidsmarge van de trend van het gemiddelde vóór 1993 zo groot is. Die is veel groter dan de onzekerheidsmarges bij de individuele reeksen, terwijl je juist het omgekeerde zou verwachten. Dit gebeurt ook ná 1993, maar in mindere mate waardoor het verschil toch nog significant is.
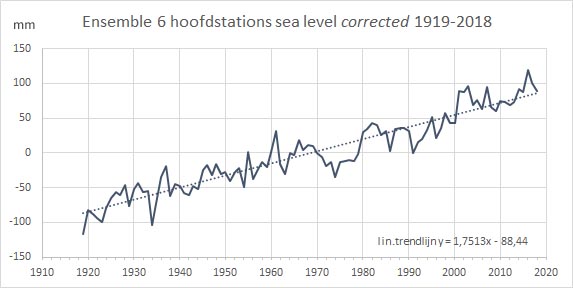
Fig.7 Reconstructie zeeniveau
In figuur 7 is de gecorrigeerde zeespiegel van Jippe Hoogeveen’s regressie weergegeven voor de 6 Nederlandse hoofdstations. De lineaire trend van de gehele reeks 1919-2018 is nu 1,75 mm/jaar, lager dan de trend uit de niet gecorrigeerde reeks van figuur 2.
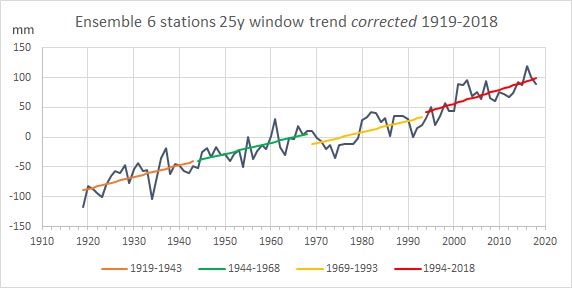
Fig.8 Reconstructie zeeniveau met trends
Om te zien of er verschillen ontstaan met de niet gecorrigeerde data is van de gecorrigeerde data de grafiek van figuur 8 gemaakt met de trend over windows van telkens 25 jaren, zoals dat ook gedaan is over de ongecorrigeerde PSMSL data in figuur 3. Voor elk van de vier 25-jarige windows is de lineaire trend bepaald en weergegeven met de gekleurde lijnstukken.
As men figuur 8 vergelijkt met figuur 3 dan is te zien dat in beide grafieken het derde window (1969-1993) uit de toon valt. In de gecorrigeerde data van figuur 8 is het echter niet zozeer de verhoogde trend van het derde window die opvalt (alle vier windows vertonen ongeveer dezelfde trend) maar de lagere waarden in de periode 1969-1993. Dat veroorzaakt een sprong aan het begin (1969) en aan het einde (1993) van dat derde window.
Conclusies: zonder dat we kunnen beschikken over de onderliggende data van de grafieken van het Delftse onderzoeksteam is vanuit diverse hoeken en perspectieven toch al behoorlijk inhoudelijk en stevig commentaar geleverd op de werkwijze van de onderzoekers. Of de nog aan te leveren data van de publicatie de geloofwaardigheid van de paper gaan verhogen valt te bezien. Omdat die data waarschijnlijk nog wel eventjes op zich laten wachten duiken we een volgende keer wat dieper in de gemeten zeespiegeldata langs onze kust.
